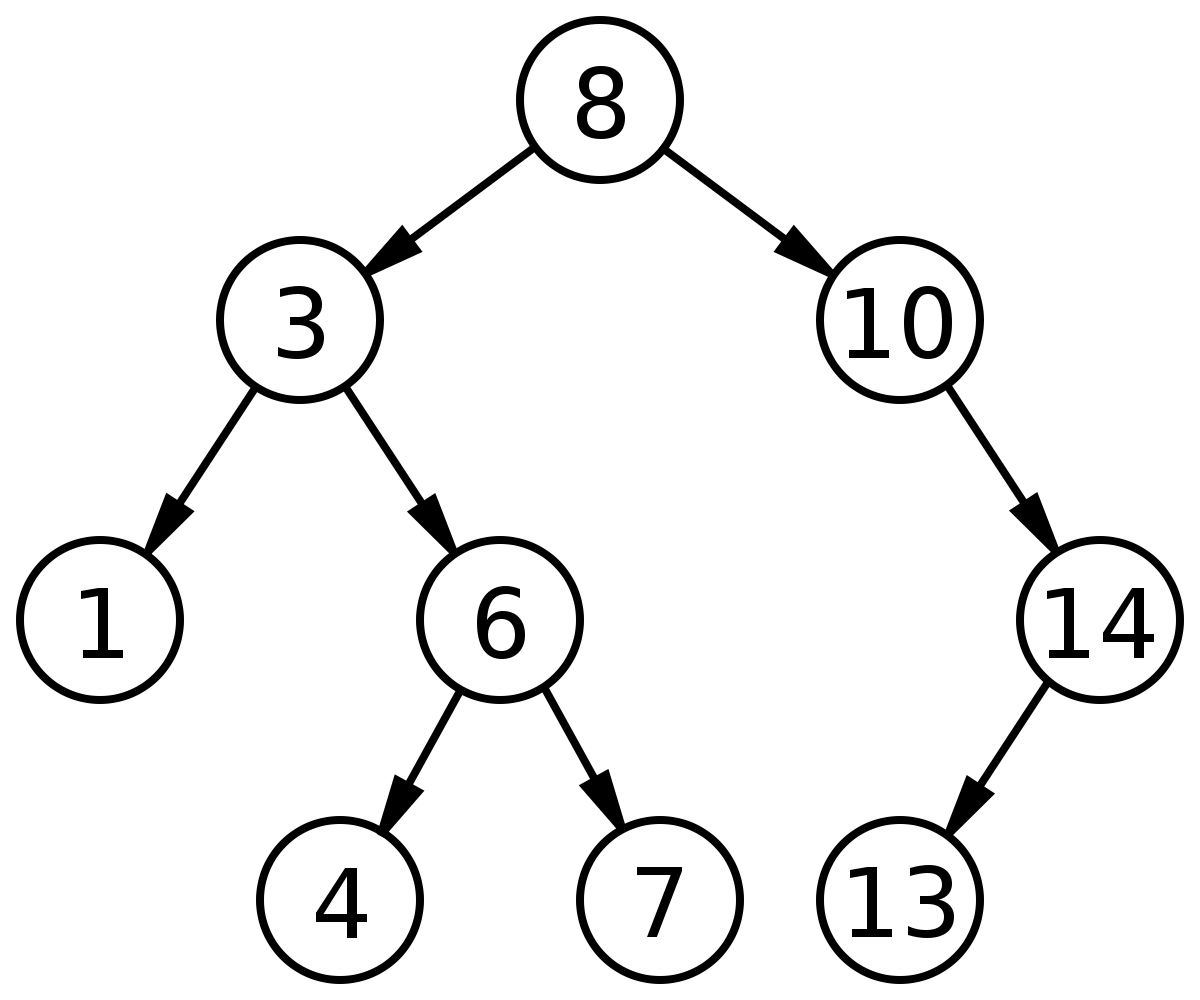
Binary Search Tree

Binary Search Tree

Binary Search Tree

Binary Search Tree adalah salah satu jenis struktur data yang memungkinkan pencarian secara cepat, melakukan sorting, serta kemudahan untuk memasukkan dan menghapus data.

Pada dasarnya Binary Search Tree adalah Binary Tree yang sudah disorting demi memudahkan pencarian data.

Konsep pada Binary Search Tree memiliki kemiripan dengan konsep Linked List, yaitu menggunakan pointer untuk menunjuk data tertentu. Jika pada Linked List terdapat head dan tail, pada BST menggunakan istilah root yang menunjuk kepada node yang paling awal dimasukkan/sebagai penentu awal. Untuk melakukan pencarian jika pada Linked List menggunakan next dan prev, namun pada BST menggunakan istilah left dan right. Left merujuk pada lokasi node yang nilainya lebih kecil dari posisi node yang dicek saat itu, sedangkan right merujuk ke lokasi node yang nilainya lebih besar. Hal yang perlu diperhatikan adalah tiap nilai dari node dalam BST tidak sama.

Operasi Pada Binary Search Tree

Pada dasarnya BST memiliki 3 metode dasar yaitu :

• Search

Metode search merupakan salah satu alasan mengapa pada BST dilakukan secara berurutan(sorting). Dengan dilakukan secara sorting besar dan kecil maka proses pencarian dapat dilakukan secara efisien dibandingkan melakukan iterasi satu per satu untuk mencari sebuah data.

Cara kerja metode search ;

1. Masukkan data yang ingin kita cari
2. Pencarian akan dilakukan dari data teratas yang akan kita jadikan sebagai root
3. Jika nilai data lebih kecil dari root maka root akan menjadi root->left dan jika lebih besar maka root akan menjadi root-> right
4. Proses pencarian dilakukan sampai data ditemukan dan akan return root agar didapatkan datanya, jika tidak ditemukan bisa di return NULL.

Code :

Contoh searching nama

• Insert

Insert adalah metode untuk memasukkan data ke dalam BST. Proses insertion di BST memperhatikan nilai dari data karena akan dipertimbangkan agar data tersorting dengan benar.

Cara kerja metode insert :

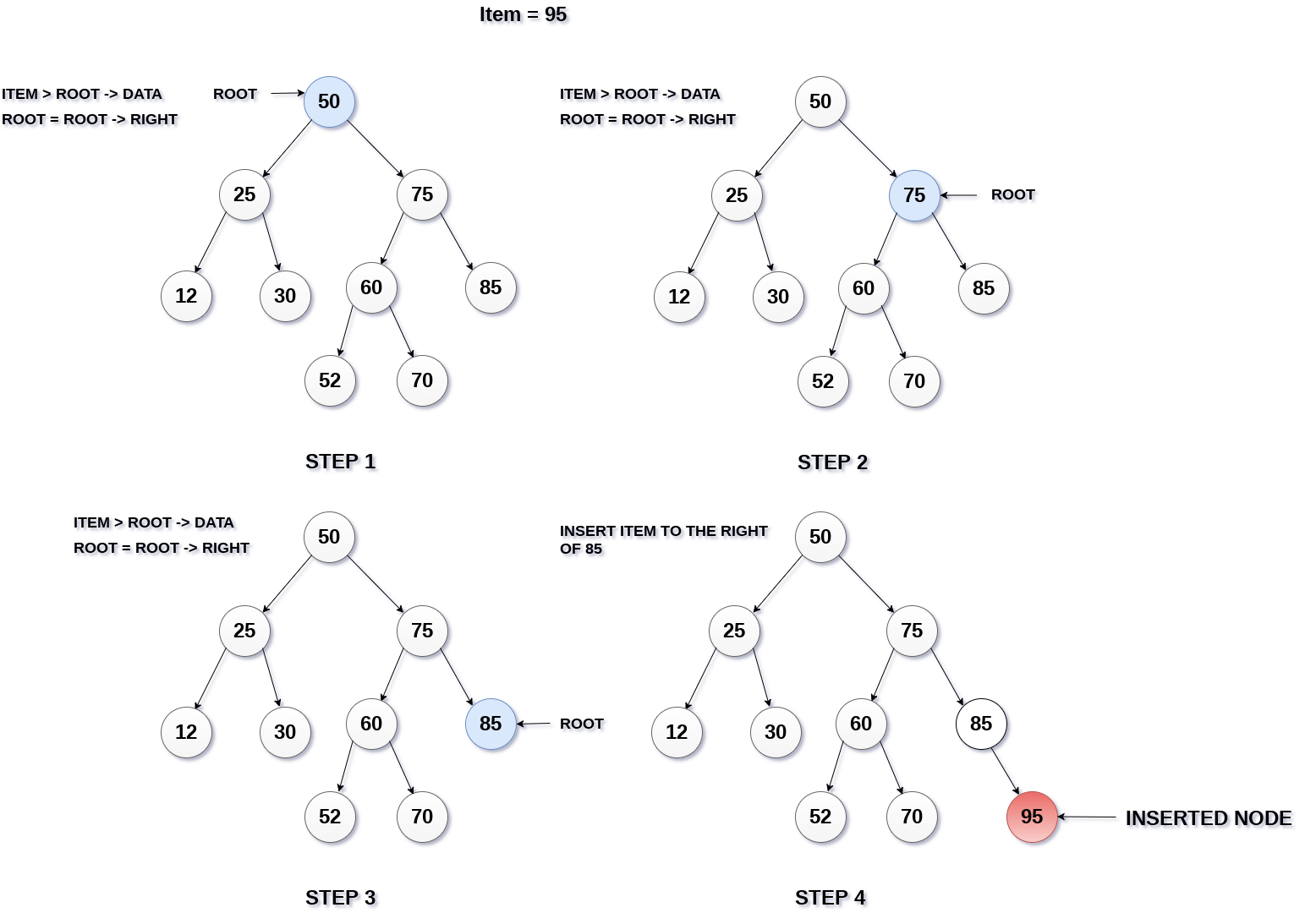
1. Akan dilakukan pengecekan terlebih dahulu apakah di posisi root NULL atau tidak
2. Jika iya maka dilakukan metode Insert
3. Jika tidak akan dicek apakah nilainya lebih besar atau kecil dari root
4. Hal tersebut dilakukan sampai ditemukan posisi root yang kosong
5. Jika ketemu posisi kosong akan dilakukan langkah ke 2

Code :

Contoh insert untuk nama

• Delete

Metode delete digunakan untuk menghapus node dalam BST.

Dalam metode delete harus dipertimbangkan node mana yang akan dihapus.

Ada 3 skenario yang perlu diperhatikan :

1. Jika node yang akan dihapus tidak memiliki child maka hapus node tersebut.
2. Jika node memiliki 1 child maka hapus node tersebut kemudian sambungkan child tersebut dengan parent dari node yang dihapus.
3. Jika node memiliki 2 child maka carilah child terkanan dari subtree kiri node, kemudian rubahlah isi dari node dengan node child terkanan tersebut kemudian hapus node child terkanan tersebut (jika ada childnya maka sambungkan dengan skenario ke 2 secara rekursif).

Code :

Contoh Delete Nama

Selain 3 metode utama diatas, ada 1 lagi metode yang bisa digunakan pada BST yaitu metode Display untuk melihat isi dari BST tersebut.

Ada 3 cara yang biasa dipakai untuk display yaitu :

• In Order : Cara display seperti ini digunakan  untuk menampilkan data secara urut (sorting)

Code :

void inOrder(Data *root){

if(root != NULL){

inOrder(root->left);

printf("%d\n",root->num);

inOrder(root->right);

}

}

• Pre Order : Cara display dengan menampilkan urutan data dari paling atas (tetap dari kiri ke kanan)

Code :

void preOrder(Data *root){

if(root != NULL){

                printf("%d\n",root->num);

preOrder(root->left);

preOrder(root->right);

}

}

• Post Order : Cara display mirip dengan in order namun yang di display bagian kanan dari subtree kiri terlebih dahulu (jika kiri sudah mentok, bergerak ke kanan sampai mentok baru diprint hasilnya)

Code :

void postOrder(Data *root){

if(root != NULL){

postOrder(root->left);

postOrder(root->right); 

                printf("%d\n",root->num);

}

}