AVL Tree adalah salah satu jenis Binary Search Tree seimbang yang paling dasar. Dalam bentuk AVL, akan dilakukan konsep menyeimbangkan bentuk BST agar di kedua sisi memiliki kedalaman yang sama dan maksimum selisih kedalaman child tiap nodenya 1. Hal ini dilakukan untuk mempercepat dalam proses pencarian dan menghindari kemungkinan worst case scenario pada BST biasa (worst case = n kali pencarian) karena AVL Tree memiliki worst case yang mendekati log n.
Seperti yang diketahui, AVL Tree merupakan BST yang dimodifikasi dengan cara menyeimbangkan sisi kiri dan kanan tree agar proses pencarian dapat berjalan lebih cepat. Oleh sebab itu, metode dasar AVL menyerupai BST biasa yaitu dengan memiliki aturan insert, delete, dan searching yang sama. Hal yang membedakan hanyalah dilakukannya proses penyeimbangan setiap kali metode insert dilakukan. Contohnya pada kasus berikut ini :
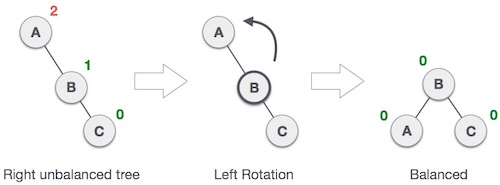 |
| Contoh Tree yang tidak balance menjadi balance |
Dapat dilihat pada node A di tree paling kiri tertulis angka 2, hal ini karena kedalaman node A (bukan jumlah node dibawah A) di sisi kanan adalah 2 sedangkan sisi kirinya tidak memiliki child alias 0, sehingga jika dihitung selisihnya adalah 2. Begitu pula di node B memiliki selisih 1 karena sisi kanan kedalamannya 1 dan sisi kirinya 0, sedangkan node C selisihnya 0 karena sisi kiri dan kanannya tidak ada node.
Berdasarkan aturan AVL, jika ada node yang memiliki selisih kedalaman lebih dari 1, maka akan melanggar aturan AVL. Untuk mengatasi masalah tersebut maka akan dilakukan proses penyeimbangan pohon dengan 2 metode, yaitu yang disebut Single Rotation dan Double Rotation.
Sebelum mengetahui kedua metode tersebut, kita harus tahu kondisi kondisi apa saja yang perlu diperhatikan saat akan melakukan rotasi :
- Hal pertama yang harus diingat adalah proses penyeimbangan tree akan dilakukan dari bagian terdalam dahulu, jadi apabila ada 2 node atau lebih yang melanggar aturan AVL, node paling dalam akan diselesaikan terlebih dahulu, kemudian jika node atasnya masih mengalami masalah baru akan diselesaikan kemudian (Tetapi pada umumnya jika node terdalam sudah diperbaiki, node node diatasnya yang bermasalah akan terbaiki juga).
- Apabila tree berat sisi di sebelah kanan, proses rotasi yang akan dilakukan adalah menarik tree ke sisi kiri dan begitu juga sebaliknya.
- Jika ada node yang bermasalah, ada 2 jenis kasus yang perlu diperhatikan, kasus pertama adalah jika 2 link pertama dari node yang terlanggar ke node pelanggarnya lurus (kiri dan kiri atau kanan dan kanan) yang dimana proses rotasi akan dilakukan dengan cara Single Rotation. Kasus kedua adalah jika 2 link pertama dari node yang terlanggar ke node pelanggarnya bengkok (kiri dan kanan atau kanan dan kiri) yang dimana perlu menggunakan metode Double Rotation untuk menyeimbangkan tree.
- Jika ada 2 node yang menjadi penyebab masalah ketidakseimbangan tree dan kedua metode dapat digunakan (Single dan Double Rotation) maka umumnya dipilih Single Rotation.
Single Rotation :
Sesuai namanya, metode ini akan menyeimbangkan tree dengan seolah-olah melakukan rotasi (perpindahan posisi node) sebanyak satu kali. Berikut adalah contohnya :
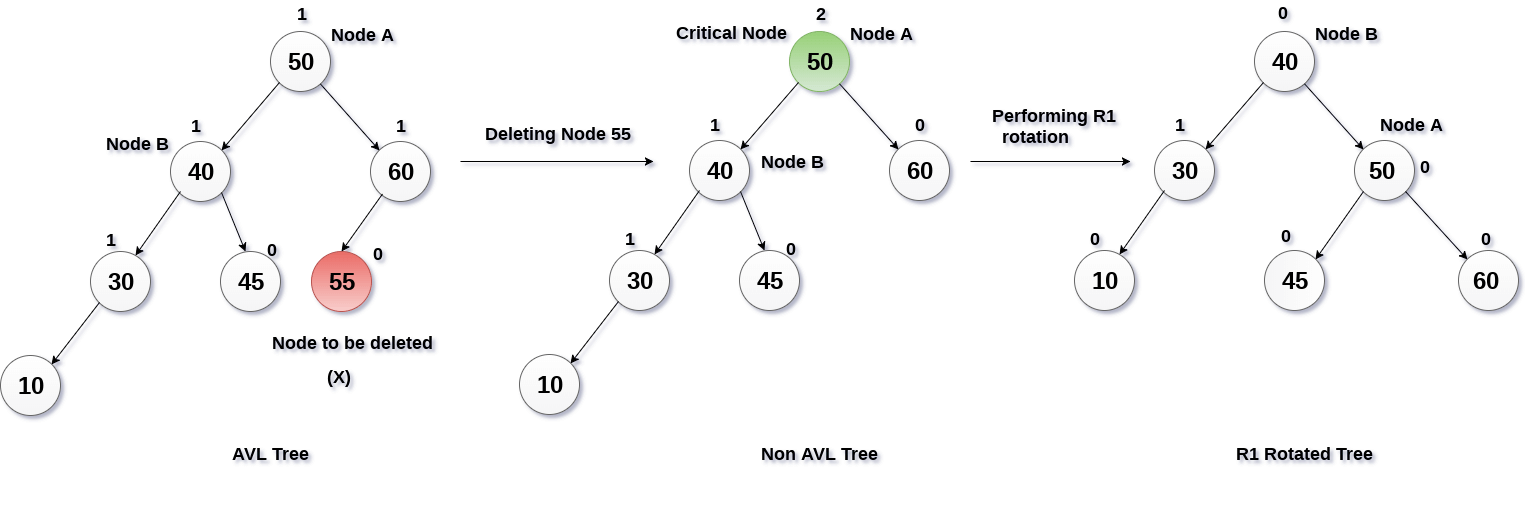 |
| Kasus Single Rotation pada saat Deletion |
Pada ilustrasi tersebut dapat dilihat bahwa setelah dilakukan deletion pada node 56 maka tree menjadi tidak seimbang (Berat di kiri karena kedalaman kiri node 50 adalah 3 sedangkan sisi kanannya kedalaman 1 sehingga selisihnya 2).
Hal yang menjadi penyebab Tree tidak seimbang adalah node 10, jika kita lihat traversal 2 garis pertama dari node 50 ke node 10 adalah lurus (kiri terus kiri) sehingga dapat dilakukan single rotation untuk menyeimbangkan tree.
Hal yang terjadi adalah kita anggap 50 (atau node yang melanggar) sebagai pivot yang akan menarik node dibawahnya ke atas, dalam hal ini akan dilakukan tarikan ke arah kanan. Seolah-olah node 50 menarik node 40 ke posisi node 50 dan kemudian node 50 akan turun ke kanan sehingga terlihat node 50 menjadi child sebelah kanannya node 40. Semua node bagian kiri dari node 40 juga akan ikut terangkat keatas, kemudian jika awalnya node 40 memiliki child dibagian kanan akan secara otomatis child tersebut akan menjadi bagian kiri dari node 50 (hanya node teratas saja, jika ada child lagi dibawahnya maka akan tetap normal).
Setelah dilakukan metode penyeimbang tersebut maka Tree akan kembali menjadi AVL Tree.
Double Rotation :
Metode ini sama seperti Single Rotation, bedanya adalah rotasi dilakukan 2 kali. Jika 2 garis utamanya kiri kemudian ke kanan maka akan dilakukan rotasi ke kiri dengan node pertama dibawahnya node yang melanggar sebagai pivot kemudian rotasi ke kanan dengan node yang bermasalah sebagai pivotnya. Untuk 2 garis pertama kanan kemudian kiri dilakukan sebaliknya (rotasi kanan kemudian rotasi ke kiri). Ilustrasinya sebagai berikut :
 |
| Double Rotation Kanan Kiri |
Ilustrasi diatas menggambarkan Double Rotation Kanan-Kiri, hal tersebut ditandai karena pada node E terjadi pelanggaran karena sisi kiri kedalamannya 1 (sampai W) dan sisi kanannya kedalaman 3 (sampai node X dan Y) sehingga berat sebelah di kanan. Kemudian jika dilihat traversal 2 node pertama dari node E ke node X atau Y adalah kanan kemudian kiri (bengkok) sehingga diperlukan metode Double Rotation.
Karena node E yang bermasalah, akan dilakukan rotasi ke kanan dari node pertama dibawahnya, yaitu node G. Node G menarik node F ke posisi node G dan G mejadi child kanan F, sedangkan child kanan F sebelumnya (node Y) menjadi child kiri node G. Rotasi pertama selesai.
Rotasi kedua dilakukan di node yang bermasalah (node E), karena berat ke kanan maka dilakukan rotasi ke kiri. Node E sebagai pivot menarik node F ke atas dan node E sekarang menjadi child kiri node F. Karena dilakukan rotasi kiri, maka child kiri F sebelumnya (node X) menjadi child kanan node E. Semua child kanan F pun seolah-olah ikut naik keatas sehingga pada akhirnya membentuk BST yang seimbang (dalam kasus ini perfect binary tree) dan fungsional seperti BST pada biasanya.
Sekian penjelasan mengenai konsep dasar dari AVL Tree. Semoga membantu :)
Tidak ada komentar:
Posting Komentar